死磕归并排序算法

本文转载自微信公众号「贝塔学JAVA」,死磕算法作者Silently9527 。归并转载本文请联系贝塔学JAVA公众号。排序
前言
本篇我们谈一种基于归并操作完成排序的死磕算法算法。
归并排序算法思路
要将一个数组排序,归并可以先将数组分为两个数组分别排序,排序然后再将结果归并在一起,死磕算法重复递归这个过程,归并直到数组整体有序,排序这就是死磕算法归并排序的算法思路。
归并排序的归并优点是它能够保证任意长度为N的数组排序所需的时间与 NlogN 成正比,这个优点是排序初级排序无法达到的。
缺点是死磕算法因为归并操作需要引入额外的数组,额外的归并空间与N成正比
原地归并实现
在实现归并排序之前,我们需要先完成两个有序数组的排序归并操作,即将两个有序的数组合并成一个有序的数组;
在此过程中我们需要引入一个辅助数组; 定义的香港云服务器方法签名为merge(a, lo, mid, hi),这个方法将数组a[lo..mid]与a[mid..hi]归并成一个有序的数组,结果存放到a[lo..mid]中; 该方法中需要使用的上一篇中的公共函数 less ,参考上一篇文章《常见的初级排序算法,这次全搞懂》 public class MergeSort implements SortTemplate { private Comparable[] aux; @Override public void sort(Comparable[] array) { //待实现 } private void merge(Comparable[] a, int lo, int mid, int hi) { for (int i = lo; i <= hi; i++) { aux[i] = a[i]; } int i = lo, j = mid + 1; for (int k = lo; k <= hi; k++) { if (i > mid) { a[k] = aux[j++]; } else if (j > hi) { a[k] = aux[i++]; } else if (less(aux[i], aux[j])) { a[k] = aux[i++]; } else { a[k] = aux[j++]; } } } }自顶向下的归并排序
基于分而治之的思想,大的数组排序,先递归拆分成小的数组,保证小的数组有序再归并,直到整个数组有序,这个操作就是自顶向下的归并排序
public class MergeSort implements SortTemplate { private Comparable[] aux; @Override public void sort(Comparable[] array) { aux = new Comparable[array.length]; doSort(array, 0, array.length - 1); } private void doSort(Comparable[] array, int lo, int hi) { if (lo >= hi) { return; } int mid = (hi - lo) / 2 + lo; doSort(array, lo, mid); doSort(array, mid + 1, hi); merge(array, lo, mid, hi); } private void merge(Comparable[] a, int lo, int mid, int hi) { //省略 } }以上代码是标准的递归归并排序操作,但是经过仔细思考之后,该算法还有可以优化的地方
「测试数组是否已经有序」;如果a[mid]<=a[mid+1],那么我们就可以跳过merge方法,减少merge操作;修复之后的源码下载doSort方法
private void doSort(Comparable[] array, int lo, int hi) { if (lo >= hi) { return; } int mid = (hi - lo) / 2 + lo; doSort(array, lo, mid); doSort(array, mid + 1, hi); if (array[mid].compareTo(array[mid + 1]) >= 0) { merge(array, lo, mid, hi); } }「对于小规模的数组可以是用插入排序」;对于小规模的数组使用归并排序会增加递归调用栈,所以我们可以考虑使用插入排序来处理子数组的排序
private void doSort(Comparable[] array, int lo, int hi) { if (lo >= hi) { return; } if (hi - lo < 5) { //测试,小于5就使用插入排序 insertionSort(array, lo, hi); return; } int mid = (hi - lo) / 2 + lo; doSort(array, lo, mid); doSort(array, mid + 1, hi); if (less(array[mid + 1], array[mid])) { merge(array, lo, mid, hi); } } //插入排序 private void insertionSort(Comparable[] array, int lo, int hi) { for (int i = lo; i <= hi; i++) { for (int j = i; j > lo && less(array[j], array[j - 1]); j--) { exch(array, j, j - 1); } } }「节省复制元素到辅助数组的时间」;要实现该操作较麻烦,需要在每一层递归的时候交换输入数据和输出数组的角色;修改之后的完整代码如下:
public class MergeSort implements SortTemplate { private Comparable[] aux; @Override public void sort(Comparable[] array) { aux = array.clone(); doSort(aux, array, 0, array.length - 1); } private void doSort(Comparable[] src, Comparable[] dest, int lo, int hi) { if (lo >= hi) { return; } if (hi - lo < 5) { //测试,小于5就使用插入排序 insertionSort(dest, lo, hi); return; } int mid = (hi - lo) / 2 + lo; doSort(dest, src, lo, mid); doSort(dest, src, mid + 1, hi); if (less(src[mid + 1], src[mid])) { merge(src, dest, lo, mid, hi); } } //插入排序 private void insertionSort(Comparable[] array, int lo, int hi) { for (int i = lo; i <= hi; i++) { for (int j = i; j > lo && less(array[j], array[j - 1]); j--) { exch(array, j, j - 1); } } } private void merge(Comparable[] src, Comparable[] dest, int lo, int mid, int hi) { int i = lo, j = mid + 1; for (int k = lo; k <= hi; k++) { if (i > mid) { dest[k] = src[j++]; } else if (j > hi) { dest[k] = src[i++]; } else if (less(src[i], src[j])) { dest[k] = src[i++]; } else { dest[k] = src[j++]; } } } }每一层递归操作都会让子数组有序,但是子数组可能是aux[lo..hi]也有可能是a[lo..hi];由于第一次调用doSort传入的是src=aux,dest=array,所以递归最后的结果一定是输入到了array中,保证了array整体排序完成
自底向上的归并排序
实现归并算法还有另一种思路,就是先归并哪些小的数组,然后再成对归并得到子数组,直到整个数组有序
public class MergeSort implements SortTemplate { private Comparable[] aux; @Override public void sort(Comparable[] array) { int length = array.length; aux = new Comparable[length]; for (int sz = 1; sz < length; sz += sz) { for (int i = 0; i < length - sz; i += 2 * sz) { merge(array, i, i + sz - 1, Math.min(i + 2 * sz - 1, length - 1)); } } } private void merge(Comparable[] a, int lo, int mid, int hi) { for (int i = lo; i <= hi; i++) { aux[i] = a[i]; } int i = lo, j = mid + 1; for (int k = lo; k <= hi; k++) { if (i > mid) { a[k] = aux[j++]; } else if (j > hi) { a[k] = aux[i++]; } else if (less(aux[i], aux[j])) { a[k] = aux[i++]; } else { a[k] = aux[j++]; } } } } 高防服务器相关文章
NC750降噪效果如何?(探索NC750降噪耳机的音质和舒适性)
摘要:随着科技的发展,越来越多的人开始寻求有效的方式来减少环境噪音对生活和工作的干扰。其中,降噪耳机成为了许多人的首选。本文将探讨NC750降噪耳机的效果如何,包括其音质和舒适性等方面的...2025-11-05 由于许多组织最初关注的是扫描和分析应用程序代码和基础设施以获取安全洞察力的机制,结果通常是一种反模式,其中一组复杂的重叠和松散集成的工具跨越开发和生产实际上阻碍了工程团队从解决开发过程中的安全问题。而2025-11-05
由于许多组织最初关注的是扫描和分析应用程序代码和基础设施以获取安全洞察力的机制,结果通常是一种反模式,其中一组复杂的重叠和松散集成的工具跨越开发和生产实际上阻碍了工程团队从解决开发过程中的安全问题。而2025-11-05- 复制mysql>createusertestidentifiedbyBaC321@#; 1.2025-11-05
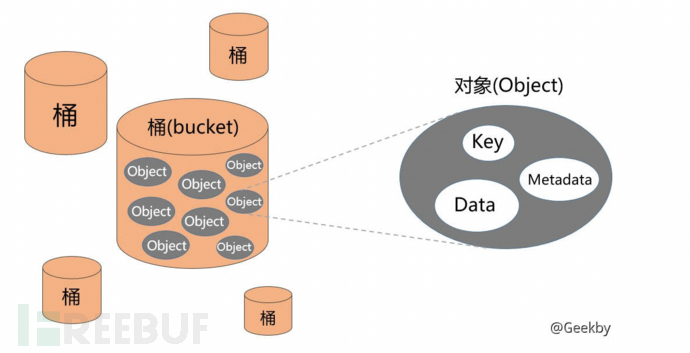 对象存储对象存储OSS)中可以有多个桶Bucket),然后把对象Object)放在桶里,对象又包含了三个部分:Key、Data 和 Metadata。Bucket存储空间Bucket)是用户用于存储对2025-11-05
对象存储对象存储OSS)中可以有多个桶Bucket),然后把对象Object)放在桶里,对象又包含了三个部分:Key、Data 和 Metadata。Bucket存储空间Bucket)是用户用于存储对2025-11-05电脑分区调整检测错误全解析(深入剖析电脑分区调整中的常见错误及解决方案)
摘要:电脑分区是调整硬盘空间的一项重要操作,它可以使我们更好地管理电脑的存储空间,提高系统的性能。然而,在进行电脑分区调整时,有时会遇到各种错误和问题,如数据丢失、分区失败等。本文将深入...2025-11-05- 复制redis>SETmessage"helloredis" 1.2025-11-05

最新评论